A2
Many calculations are made easier using ideal gases. These make assumptions:
- Molecules are in rapid, random motion
- All collisions are elastic
- Gravitational forces on molecules are negligible
- There are no intermolecular forces except during collisions
- The total volume of the molecules is negligible compared to the volume of the container
A number of laws apply for ideal gases:
Boyle’s law

at constant temperature (isothermal conditions)
This breaks down for real gases at high pressure, as atom volume becomes significant in comparison to container volume.
Pressure law

at constant volume (isochoric conditions)
Charles’ law

at constant pressure (isobaric conditions)
The ideal gas equation
These three laws can be combined to form one equation, the ideal gas equation:

n is the number of moles of the gas (a measure of amount) and R is the molar gas constant.
This is most commonly written as:
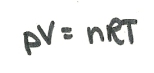
University
The ideal gas law can be represented on a p-V graph:

The lines are called isotherms, as on one line all the points are at the same temperature.
In reality, the graph looks a bit different:

This is due to the interactions between the molecules, and the volume of the molecules. This is particularly noticeable at lower temperature, so the lower isotherms affected much more.
Gases are also compressible. This is given the letter z, and z is 1 for an ideal gas. Otherwise:
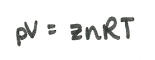
The compressibility changes: at high pressure z increases as molecules take up more space, and at low pressure z may decrease due to attractive interactions between the molecules (they become closer together so are less easy to compress more). Compressibility changes differently for different gases:

A better way to describe gases is using Van Der Waal’s equation:

a represents the attractive forces in the gas (so increases with molecular size) and b represents the volume of a mole of gas molecules (so also increases with molecular size).
If we rearrange the equation the volume correction and interactive force correction can be seen:

